cbx.objectives.cross_in_tray#
- class cbx.objectives.cross_in_tray[source]#
Bases:
cbx_objectiveCross-In-Tray function
The Cross-In-Tray function is a function with many local minima and one global minimum [1]. It is defined as
\[f(x,y) = -0.0001 \left( \left| \sin(x) \sin(y) \exp \left( \left| 100 - \frac{\sqrt{x^2 + y^2}}{\pi} \right| \right) + 1 \right| + 1 \right)^0.1,\]see [1].
- Parameters:
None
Global minima#
\(f(x,y) = -2.06261\) at \((x,y) = (1.34941, 1.34941)\)
\(f(x,y) = -2.06261\) at \((x,y) = (-1.34941, -1.34941)\)
\(f(x,y) = -2.06261\) at \((x,y) = (1.34941, -1.34941)\)
\(f(x,y) = -2.06261\) at \((x,y) = (-1.34941, 1.34941)\)
Examples
>>> import numpy as np >>> from cbx.objectives import cross_in_tray >>> x = np.array([[1,2], [3,4], [5,6]]) >>> f = cross_in_tray() >>> f(x)
Visualization#
(
Source code,png,hires.png,pdf)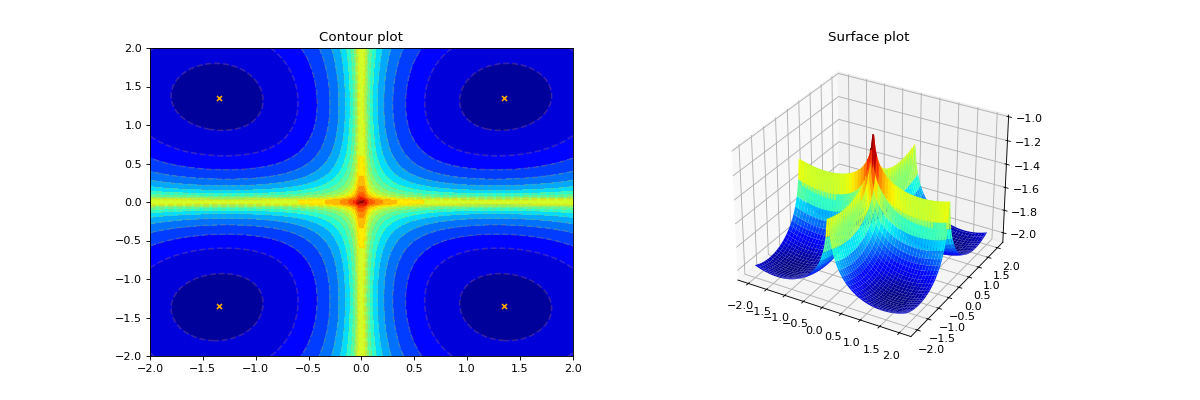
References
