cbx.objectives.Holder_table#
- class cbx.objectives.Holder_table(factor=1.0, shift=0)[source]#
Bases:
cbx_objectiveHolder table
The Holder table function is a function with many local minima and four global minima [1]. It is defined as
\[f(x,y) = -\left| \sin(x) \cos(y) \exp \left( \left| 1 - \frac{\sqrt{x^2 + y^2}}{\pi} \right| \right) \right|,\]and its domain is \([-10,10]^2\). Note, that this function can decrease further if the domain is enlarged.
- Parameters:
None
Global minima#
\(f(x,y) = -19.2085\) at \((x,y) = (8.05502, 9.66459)\)
\(f(x,y) = -19.2085\) at \((x,y) = (-8.05502, 9.66459)\)
\(f(x,y) = -19.2085\) at \((x,y) = (8.05502, -9.66459)\)
\(f(x,y) = -19.2085\) at \((x,y) = (-8.05502, -9.66459)\)
Examples
>>> import numpy as np >>> from cbx.objectives import Holder_table >>> x = np.array([[1,2], [3,4], [5,6]]) >>> f = Holder_table() >>> f(x)
Visualization#
(
Source code,png,hires.png,pdf)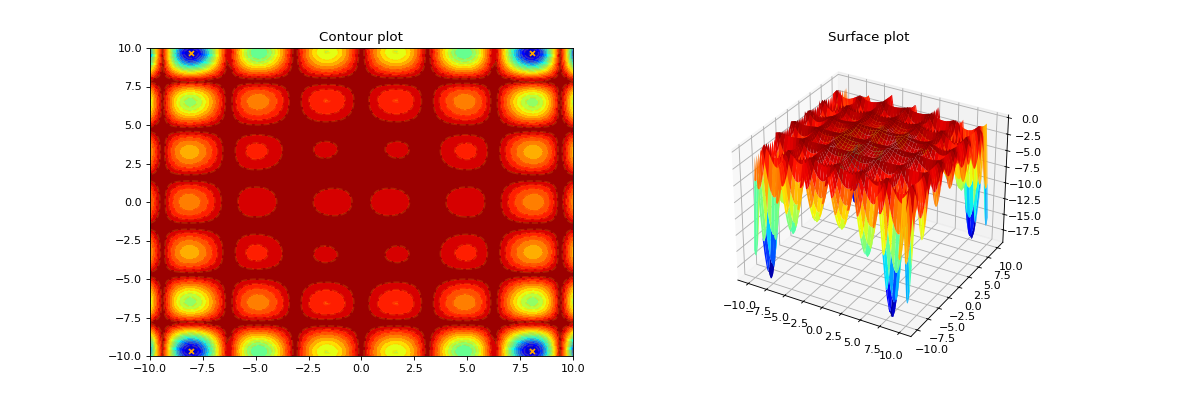
References
