cbx.objectives.Rastrigin#
- class cbx.objectives.Rastrigin(b=0.0, c=0.0, A=10.0)[source]#
Bases:
cbx_objectiveRastrigin’s function
Rastrigin’s function is a multimodal function with a global minima at \((0,0)\). The function is originally defined on \(\mathbb{R}^2\) as
\[f(x,y) = (x^2 + y - 11)^2 + (x + y^2 - 7)^2.\]See Rastrigin’s function. For our case we employ a shifted version on \(\mathbb{R}^d\), where the global minimum is at \((b)\) and we additonally employ a offset \(c\),
\[\tilde{f}(x,y) = \frac{1}{n} \sum_{i=1}^n \left[ (x_i - b)^2 - 10 \cos(2 \pi (x_i - b)) + 10 \right] + c.\]- Parameters:
b (float, optional) – The first parameter of the function. The default is 0.0.
c (float, optional) – The second parameter of the function. The default is 0.0.
Examples
>>> import numpy as np >>> from cbx.objectives import Rastrigin >>> x = np.array([[1,2], [3,4], [5,6]]) >>> f = Rastrigin() >>> f(x) array([ 68., 148., 1556.])
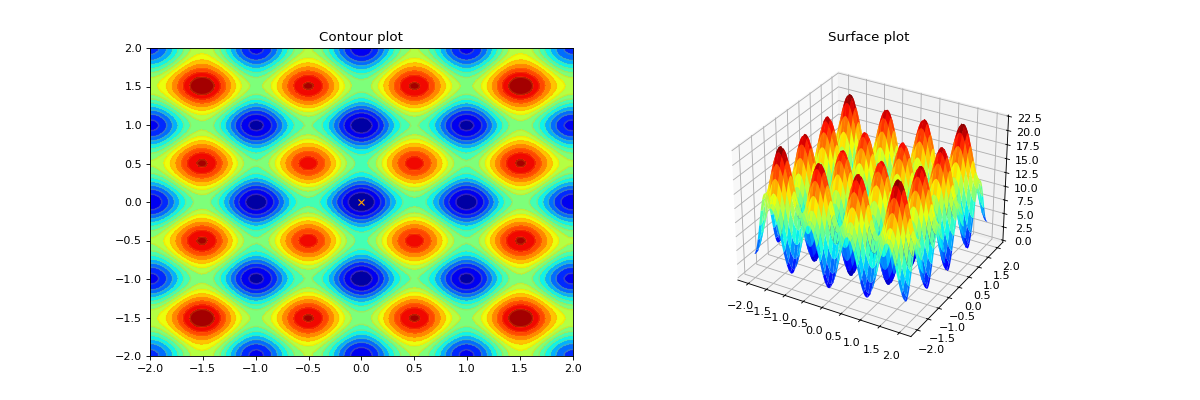
Visualization#
(
Source code,png,hires.png,pdf)